0 1背包问题

01给定 $n$ 个物品，第 $i$ 个物品的重量为 $wgt[i-1]$ 、价值为 $val[i-1]$ ，和一个容量为 $cap$ 的背包。每个物品只能选择一次，问在限定背包容量下能放入物品的最大价值。

对于每个物品来说，不放入背包，背包容量不变；放入背包，背包容量减小。由此可得状态定义：当前物品编号 i 和背包容量 c ，记为 [i,c] 。

状态 [i,c] 对应的子问题为：前 i 个物品在容量为 c 的背包中的最大价值，记为 dp[i,c] 。

待求解的是 dp[n,cap] ，因此需要一个尺寸为 (n+1)×(cap+1) 的二维 dp 表。

当我们做出物品 i 的决策后，剩余的是前 i−1 个物品决策的子问题，可分为以下两种情况。

• 不放入物品 i ：背包容量不变，状态变化为 [i−1,c] 。
• 放入物品 i ：背包容量减少 wgt[i−1] ，价值增加 val[i−1] ，状态变化为 [i−1,c−wgt[i−1]] 。

本题的最优子结构：最大价值 dp[i,c] 等于不放入物品 i 和放入物品 i 两种方案中价值更大的那一个。由此可推导出状态转移方程：

dp[i,c]=max(dp[i−1,c],dp[i−1,c−wgt[i−1]]+val[i−1])

需要注意的是，若当前物品重量 wgt[i−1] 超出剩余背包容量 c ，则只能选择不放入背包。

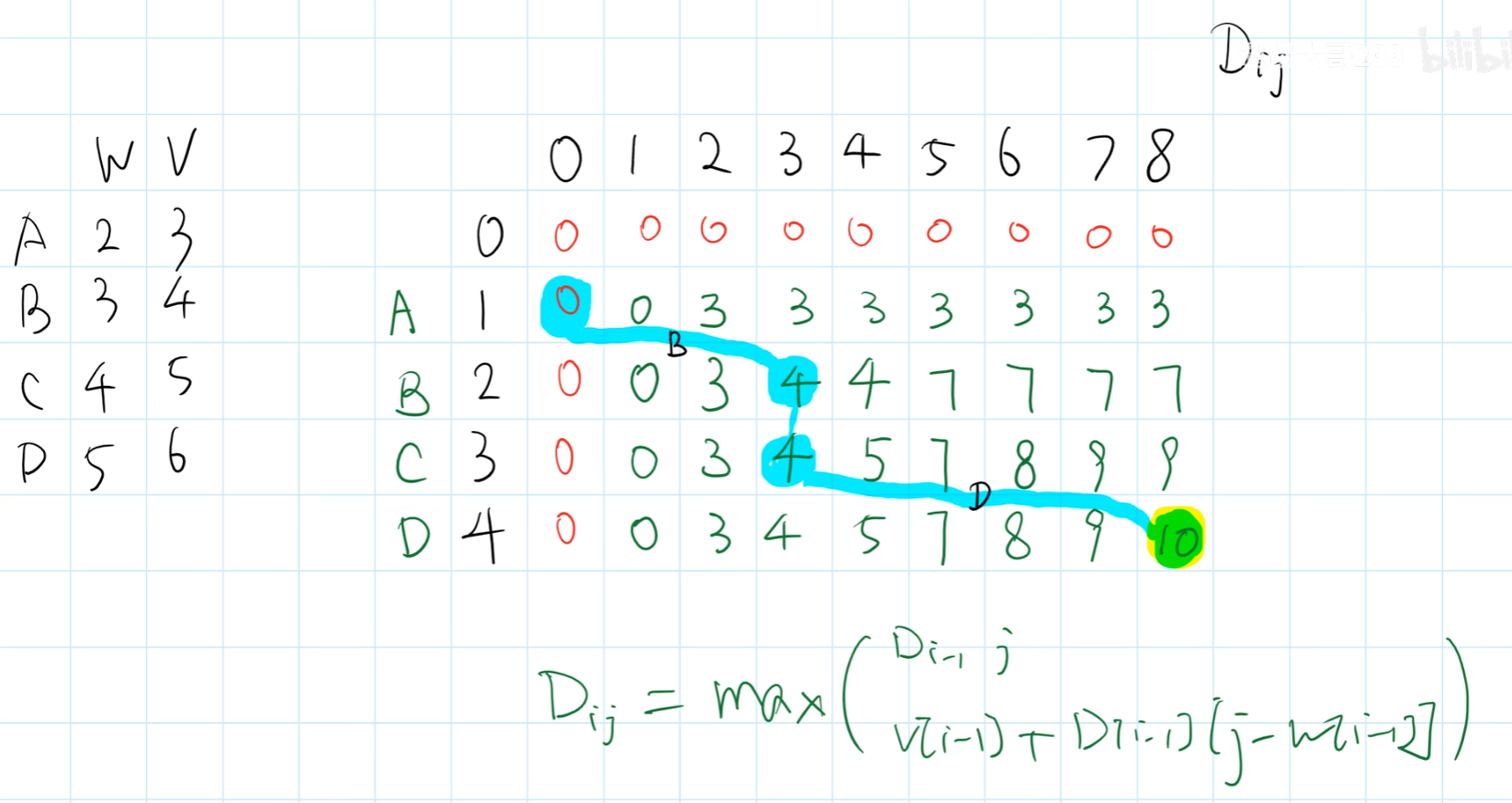
动态规划

/* 0-1 背包：动态规划 */
function knapsackDP(wgt, val, cap) {
    const n = wgt.length;
    // 初始化 dp 表
    const dp = Array(n + 1)
        .fill(0)
        .map(() => Array(cap + 1).fill(0));
    // 状态转移
    for (let i = 1; i <= n; i++) {
        for (let c = 1; c <= cap; c++) {
            if (wgt[i - 1] > c) {
                // 若超过背包容量，则不选物品 i
                dp[i][c] = dp[i - 1][c];
            } else {
                // 不选和选物品 i 这两种方案的较大值
                dp[i][c] = Math.max(
                    dp[i - 1][c],
                    dp[i - 1][c - wgt[i - 1]] + val[i - 1]
                );
            }
        }
    }
    return dp[n][cap];
}
 

reference

https://www.hello-algo.com/chapter_dynamic_programming/knapsack_problem/