Q: 什么是机器学习 A: 机器学习涉及开发数学模型，这些模型可以基于数据进行学习，并做出预测或决策，而无需进行明确的编程指令。
监督学习
Q: 什么是监督学习 A: 在一个由输入和有着打上“正确标签”的输出所组成的数据集当中，通过机器学习，达到只需输入就能得到误差很小的输出
回归模型
预测无限多可能数字中的一个
线性回归模型
用一个线性函数来预测一个模型比如: f_{w,b}(x^{(i)}) = wx^{(i)} + b \tag{1} 但问题来了，w和b有无穷多种取值，我们该如何确定这两个变量的值
此时，我们就用损失函数来代表w和b不同的取值时，这个线性函数的拟合程度，当值越小，说明预测值与实际值相差越小，当值达到最小时，误差越小，函数拟合得越好
Cost Function: J(w,b) = \frac{1}{2m} \sum\limits_{i = 0}^{m-1} (f_{w,b}(x^{(i)}) - y^{(i)})^2 \tag{1}
Q: 为什么公式中会除以二
A: 除以二对描述误差没有影响，只是人为规定，让其后面推导的公式更好看
即问题转化为求Cost Function的最小值：
如何求其最小值？
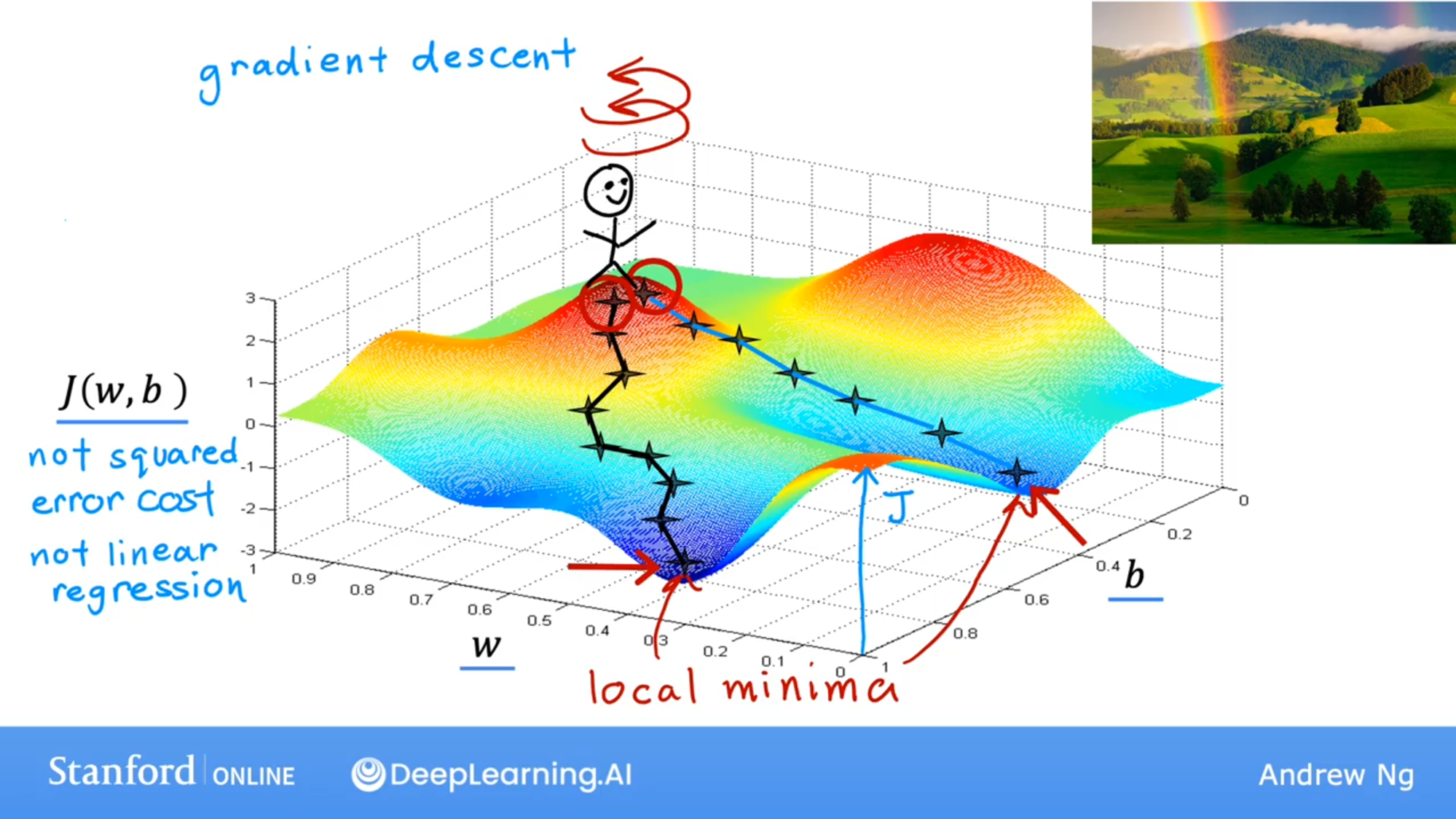这是函数，设置初始值w和b,你站在山上，然后四周环绕，观察周围的那一小步变化更大，然后踏出那一小步，然后重复上述步骤，你就会达到山谷里面，这就是梯度下降算法
即w和b都踏出那一小步：
\; w &= w - \alpha \frac{\partial J(w,b)}{\partial w} \tag{3} \; \newline b &= b - \alpha \frac{\partial J(w,b)}{\partial b} \newline \rbrace \end{align*}$$ 其中\alpha 是学习率，即每踏出一步的步伐，其中的偏导后得\begin{align}
\frac{\partial J(w,b)}{\partial w} &= \frac{1}{m} \sum\limits_{i = 0}^{m-1} (f_{w,b}(x^{(i)}) - y^{(i)})x^{(i)} \tag{4}\
\frac{\partial J(w,b)}{\partial b} &= \frac{1}{m} \sum\limits_{i = 0}^{m-1} (f_{w,b}(x^{(i)}) - y^{(i)}) \tag{5}\
\end{align}
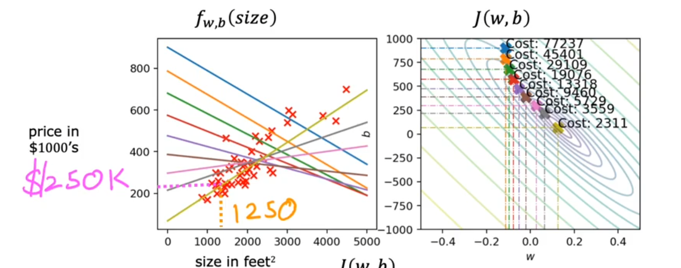 这里可以直观的看到，每一次梯度下降，w和b的焦点将无限逼近椭圆的中心原点，使得Cost Fucstion的值越来越小，w和b的取值对于这个函数拟合得越好。 但对于日常生活中复杂的模型，肯定不止只有一个变量，可能有多个变量等着我们去拟合这个函数 这怎么办呢？ ### 多元线性回归 用向量表示多个特征变量 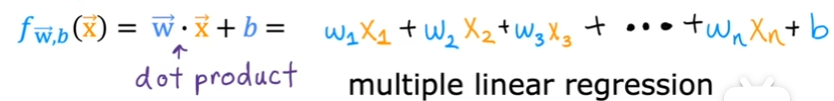 用点乘来简化： $$ f_{\mathbf{w},b}(\mathbf{x}) = \mathbf{w} \cdot \mathbf{x} + b \tag{2} $$ 这么做的优点： - 更加简洁 - 有一个库叫做Numpy它可以在硬件层面实现两个向量之间的点乘，而非用循环语句来点乘，效率大大增加  当用向量来表达时，Cost Function 变为： $$\begin{align*} \text{repeat}&\text{ until convergence:} \; \lbrace \newline\; & w_j := w_j - \alpha \frac{\partial J(\mathbf{w},b)}{\partial w_j} \tag{1} \; & \text{for j = 0..n-1}\newline &b\ \ := b - \alpha \frac{\partial J(\mathbf{w},b)}{\partial b} \newline \rbrace \end{align*}$$ 其中：\begin{align}
\frac{\partial J(\mathbf{w},b)}{\partial w_j} &= \frac{1}{m} \sum\limits_{i = 0}^{m-1} (f_{\mathbf{w},b}(\mathbf{x}^{(i)}) - y^{(i)})x_{j}^{(i)} \tag{2} \
\frac{\partial J(\mathbf{w},b)}{\partial b} &= \frac{1}{m} \sum\limits_{i = 0}^{m-1} (f_{\mathbf{w},b}(\mathbf{x}^{(i)}) - y^{(i)}) \tag{3}
\end{align}
但在生活中，向量中的每个值的取值范围差距非常大，比如只有两个特征变量，房子面积和房间数量这个例子： 它们之间的取值范围相差得很大，范围小的合理参数值可能比较大，范围大的合理参数值可能比较小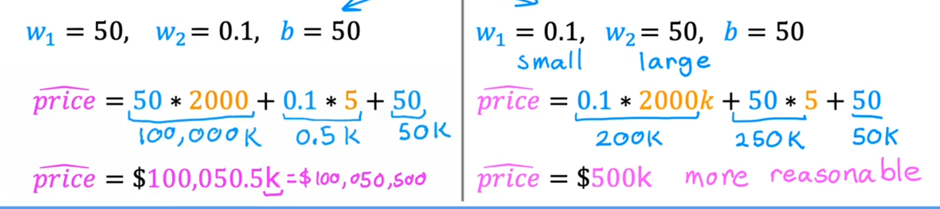：  这意味着，每当我们进行一次梯度下降的时候，w和b的值其中的一个可能会减少得非常多，导致每次梯度下降的方向不是椭圆中心方向，可以理解为：每踏一步的方向搞错了 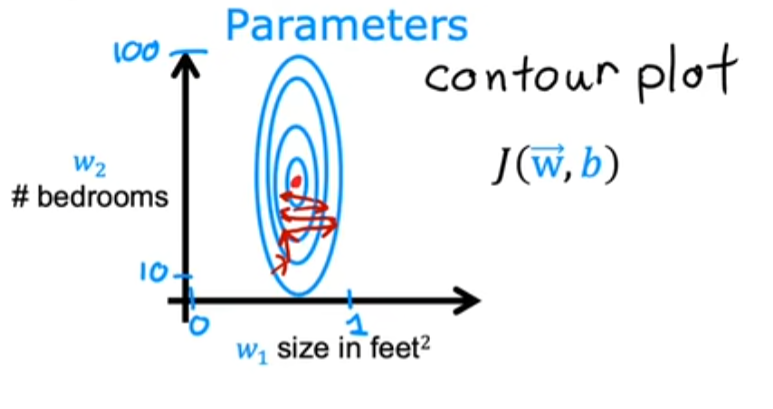 因此，我们需要特征缩放，为了让模型更公平地对待每个特征，不会因为某个特征的数值范围大就认为它更重要,可以更快的梯度下降到收敛的结果 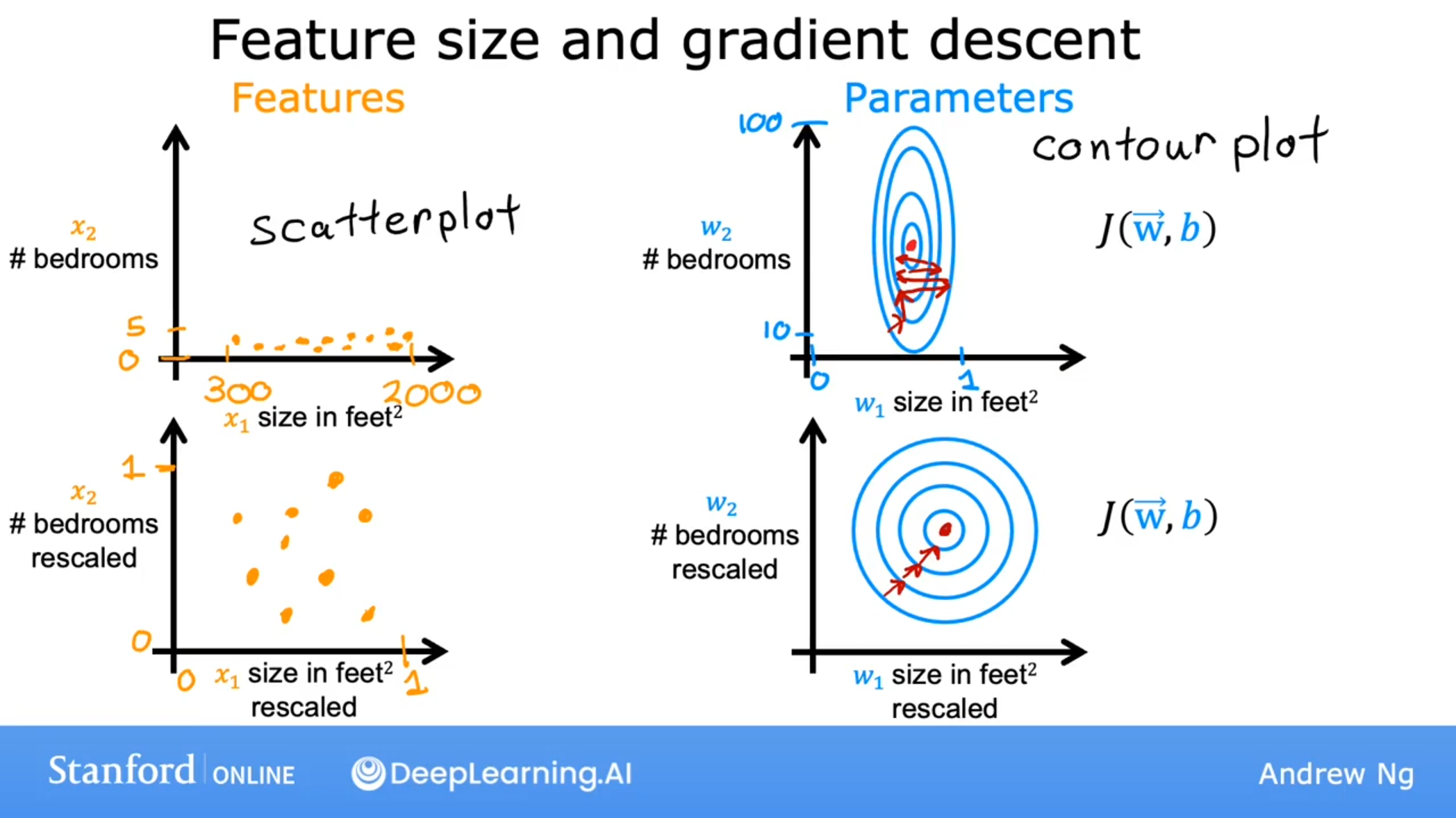 [[特征缩放]]，即把特征向量的取值范围尽量缩放到一比一的关系，即将所在的横轴坐标给缩放 #### 特征缩放实现： 1. 实现一：均值正常化 2. 实现二：Z score nomalization 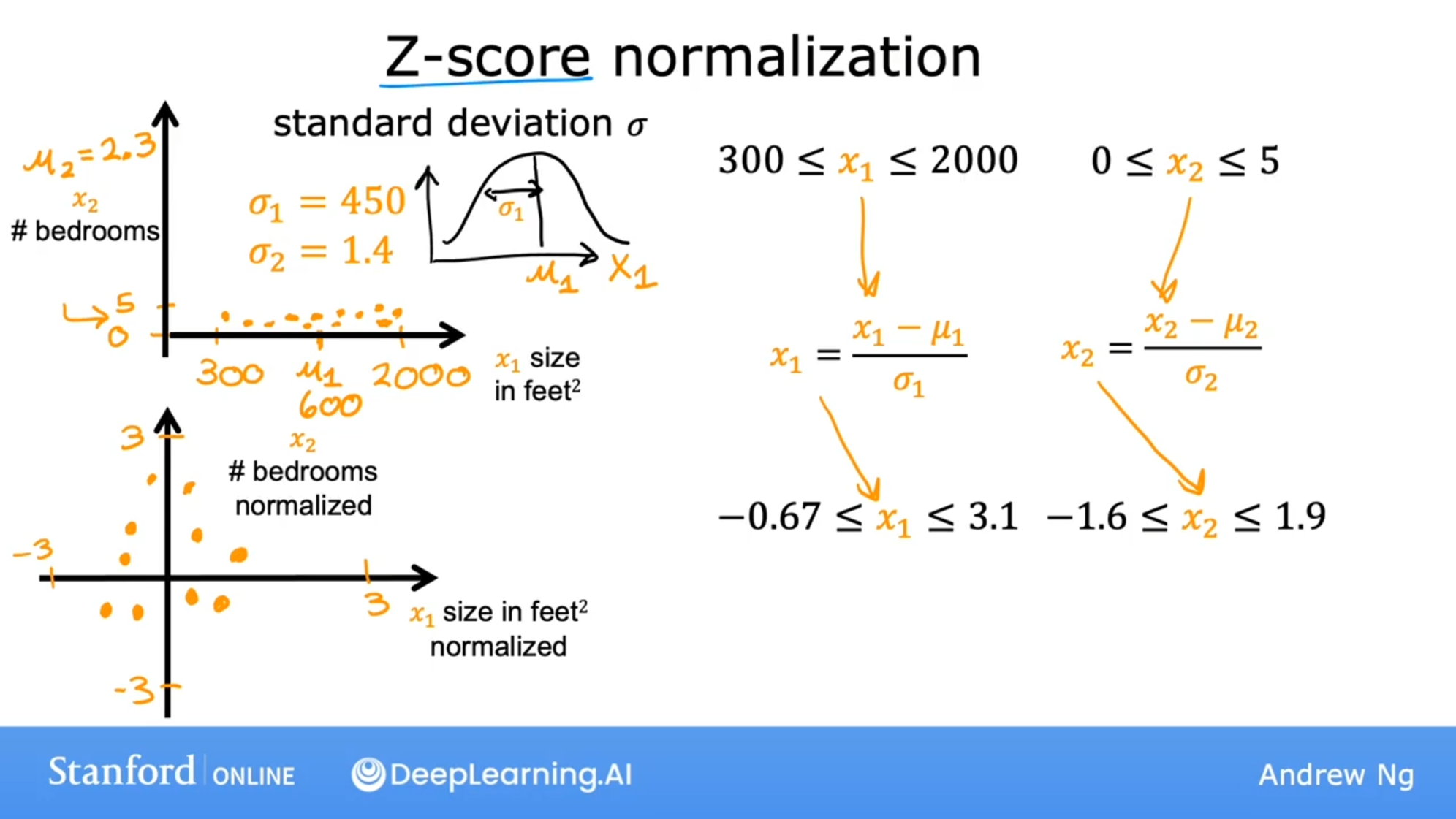 Q:那我们该如何确定这个梯度下降是收敛的呢？ A:做Cost Funcion和梯度下降迭代次数n的函数  既然每踏一步的方向确定了，踏多大的脚步呢？ ### [[学习率]]的选择 可以先取一个很小的数，看看一次梯度下降Cost Function是否减少，然后再三倍三倍的取大一点的数字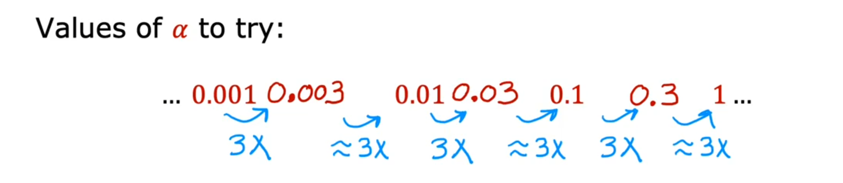 ### 特征工程 有时候需要新的特征变量来描述这个函数，而这个函数恰恰来自已有的特征变量 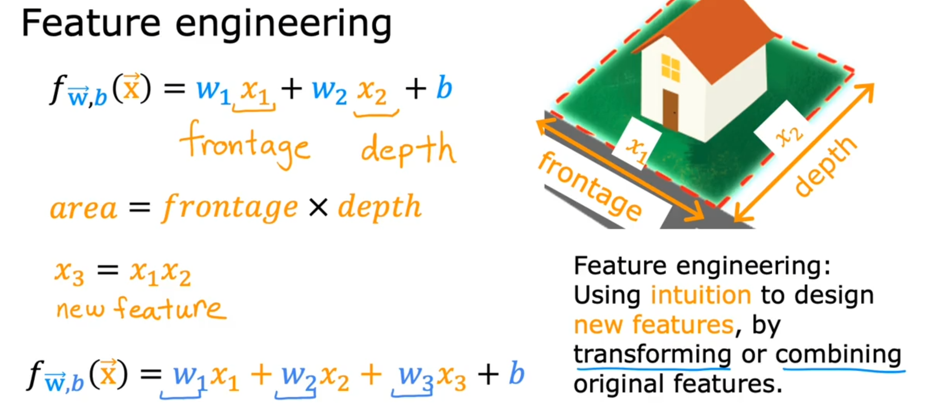 但遇到分类问题时，线性回归就不好使了，新增加数据时，会大幅度影响模型对与分类的判断 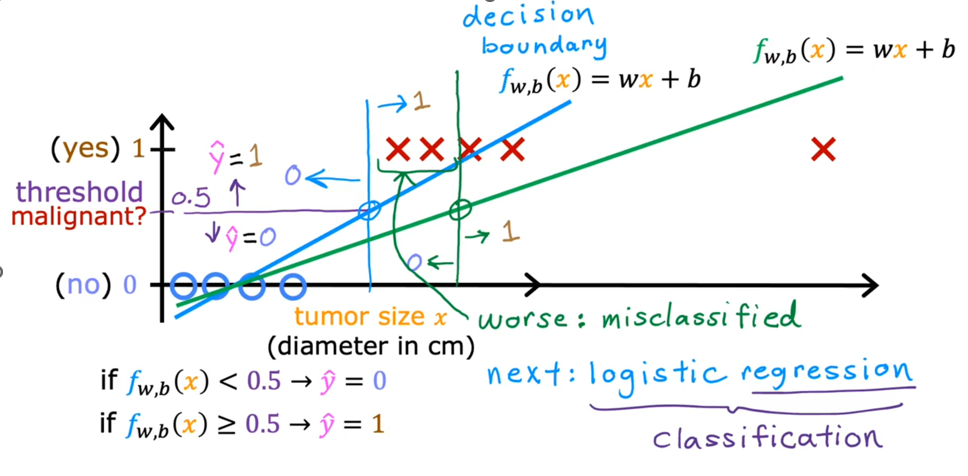 此时就应该用到分类模型 ## 分类模型 预测有限类别中的一个 ### 逻辑回归（logistic regression） 当我们预测的值只有两个：0/1 true/false yes/no 的时候，可以用激活函数（sigmoid funtion）或者逻辑函数（logistic fuction），输入特征变量，转换为函数里面的z，得到0-1的输出 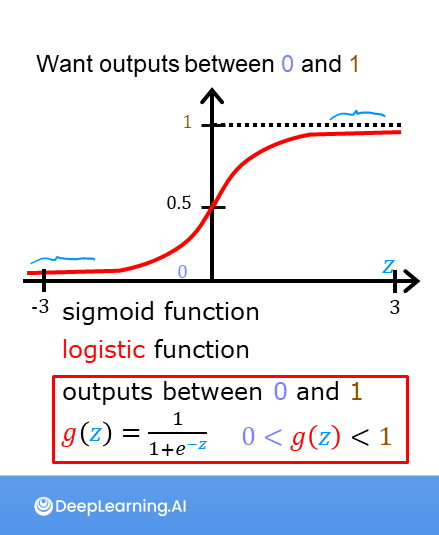 其中：\begin{align}
f_{\mathbf{w},b}(\mathbf{x^{(i)}}) &= g(z^{(i)})\tag{3} \
z^{(i)} &= \mathbf{w} \cdot \mathbf{x}^{(i)}+ b\tag{4} \
g(z^{(i)}) &= \frac{1}{1+e^{-z^{(i)}}}\tag{5}
\end{align}
就能得到这个结果： $$ f_{\mathbf{w},b}(\mathbf{x}) = g(\mathbf{w} \cdot \mathbf{x} + b ) \tag{2} $$ 我们把阈值设为0.5的话如果f>0.5,就会输出1，f<0.5时就会输出0 ### 决策边界 那当f=0.5的时候呢？此时z=0,z=0所对应w,b参数的曲线不就是**决策边界吗 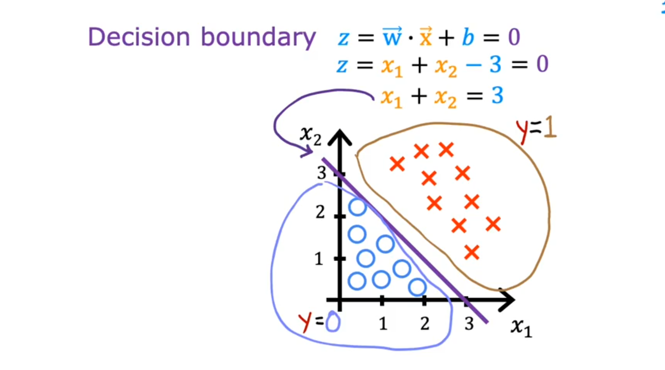 此时，相比于线性回归的话，新增加数据时，并不会影响到曲线本身 我们可以向学习线性回归那样，构造一个Cost Function,来描述平均预测值与实际值的差异，并缩小差异，找到合适的w,b参数  如果我们沿用以前一模一样的Cost Function会有什么问题？ 会导致每次梯度下降时只能找到局部最优解，而不是全局最优解 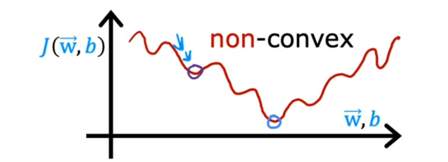 因此我们不能沿用之前的Cost Function，必须给它改造一下，把上上图中二分之一后面部分的构造一个[[损失函数]](loss function)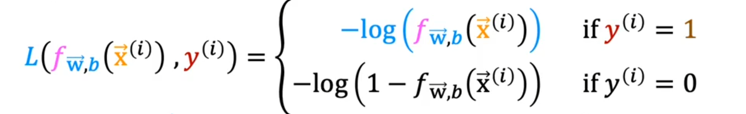：  为什么这么构造？ 我们可以看到：如果实际值为1，我把预测值取一个负对数，所得的值如果离1越近，loss function的值就越小，离1越远，loss function的值就越大，并且大得非常大，0也同理。 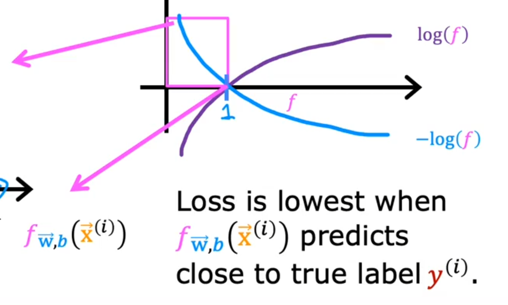 ok,得到了Loss Function 后我们需要简化一下，就得到了BinaryCrossEntropy： $$loss(f_{\mathbf{w},b}(\mathbf{x}^{(i)}), y^{(i)}) = (-y^{(i)} \log\left(f_{\mathbf{w},b}\left( \mathbf{x}^{(i)} \right) \right) - \left( 1 - y^{(i)}\right) \log \left( 1 - f_{\mathbf{w},b}\left( \mathbf{x}^{(i)} \right) \right)$$ 然后再代入Cost Function当中：$$ J(\mathbf{w},b) = \frac{1}{m} \sum_{i=0}^{m-1} \left[ loss(f_{\mathbf{w},b}(\mathbf{x}^{(i)}), y^{(i)}) \right] \tag{1}$$  现在，我们得到了Logic function当中的Cost Function,我们需要梯度下降来求得最佳的w,b的值 和线性回归的[[梯度下降]]一样： $$\begin{align*} &\text{repeat until convergence:} \; \lbrace \\ & \; \; \;w_j = w_j - \alpha \frac{\partial J(\mathbf{w},b)}{\partial w_j} \tag{1} \; & \text{for j := 0..n-1} \\ & \; \; \; \; \;b = b - \alpha \frac{\partial J(\mathbf{w},b)}{\partial b} \\ &\rbrace \end{align*}$$ 其中：$$\begin{align*} \frac{\partial J(\mathbf{w},b)}{\partial w_j} &= \frac{1}{m} \sum\limits_{i = 0}^{m-1} (f_{\mathbf{w},b}(\mathbf{x}^{(i)}) - \mathbf{y}^{(i)})x_{j}^{(i)} \tag{2} \\ \frac{\partial J(\mathbf{w},b)}{\partial b} &= \frac{1}{m} \sum\limits_{i = 0}^{m-1} (f_{\mathbf{w},b}(\mathbf{x}^{(i)}) - \mathbf{y}^{(i)}) \tag{3} \end{align*}$$ 将求好的Cost Function带入，可以得到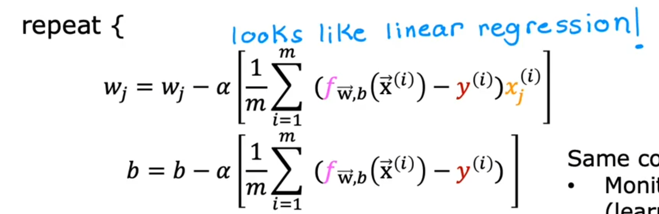：  你可能想到这个和线性回归的梯度下降看起来不是一样的吗？ 不，不一样，因为线性回归和分类回归的f函数不一样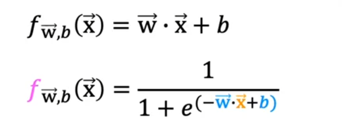：  ## [[正则化]] 恭喜你，现在你可以用线性/逻辑回归用数据去训练模型了，但还差最后一步： 当我们训练数据的时候，往往会碰到过拟合和欠拟合的情况：  欠拟合往往是特征变量太少，无法预测模型，这很简单，多添加一些特征变量就好了，但是特征变量过多或者过于复杂就会导致过拟合的情况，为什么呢?比如当我引入x的100次方这个特征变量的时候，此时这个变量对于模型影响过大，而导致了过拟合的情况，那我们该如何即能防止欠拟合，又能防止过拟合呢？ 方法一：给更多的数据 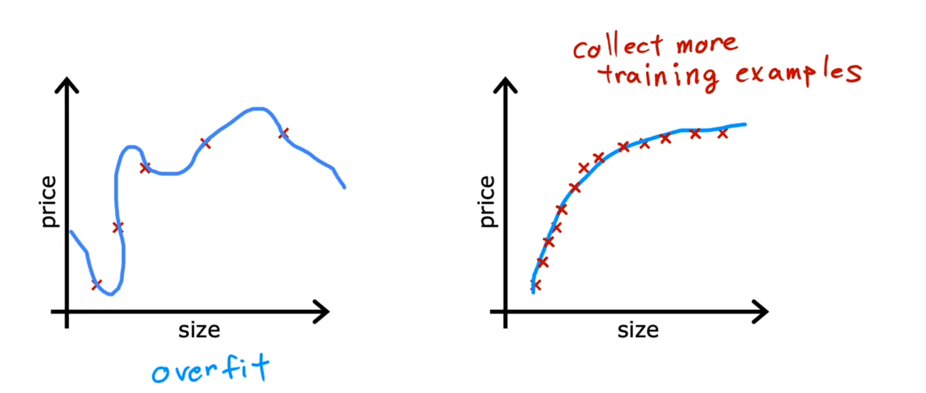 就算我给的特征变量很多很复杂，但只要我数据投喂得多，即使欠拟合，也欠拟合得刚好符合现实中的模型，但实际情况是没有这么多时间，数据可以去训练。 方法二：用直觉取用对这个模型影响非常大的特征变量 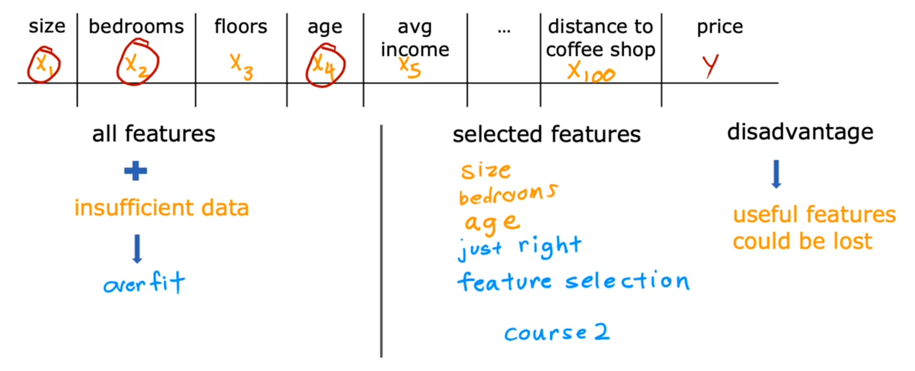 方法三：我既用很多的特征变量，但不投喂很多的数据，我把哪些对于模型影响过大的特征变量的参数w给调小，让它对模型的影响正常化。  方法三就是正则化，不过它是根据实际情况分别调小所有参数的。 ### 线性回归正则化 为了分别调小所有参数，我们可以通过变化Cost Function达到这一目的： $$J(\mathbf{w},b) = \frac{1}{2m} \sum\limits_{i = 0}^{m-1} (f_{\mathbf{w},b}(\mathbf{x}^{(i)}) - y^{(i)})^2 + \frac{\lambda}{2m} \sum_{j=0}^{n-1} w_j^2 \tag{1}$$ where: $$ f_{\mathbf{w},b}(\mathbf{x}^{(i)}) = \mathbf{w} \cdot \mathbf{x}^{(i)} + b \tag{2} $$ 其中它给Cost Function添加了参数的权重，导致我们用t梯度下降算法在计算Cost Function 最小值的时候，同时调小了那些对模型影响很大的特征变量的参数。  用同样的方法利用到逻辑回归 ### 逻辑回归正则化 $$J(\mathbf{w},b) = \frac{1}{m} \sum_{i=0}^{m-1} \left[ -y^{(i)} \log\left(f_{\mathbf{w},b}\left( \mathbf{x}^{(i)} \right) \right) - \left( 1 - y^{(i)}\right) \log \left( 1 - f_{\mathbf{w},b}\left( \mathbf{x}^{(i)} \right) \right) \right] + \frac{\lambda}{2m} \sum_{j=0}^{n-1} w_j^2 \tag{3}$$ where: $$ f_{\mathbf{w},b}(\mathbf{x}^{(i)}) = sigmoid(\mathbf{w} \cdot \mathbf{x}^{(i)} + b) \tag{4} $$ 带入梯度下降算法的公式中，可以发现，线性和逻辑回归正则化后的表达式都一样： $$\begin{align*} &\text{repeat until convergence:} \; \lbrace \\ & \; \; \;w_j = w_j - \alpha \frac{\partial J(\mathbf{w},b)}{\partial w_j} \tag{1} \; & \text{for j := 0..n-1} \\ & \; \; \; \; \;b = b - \alpha \frac{\partial J(\mathbf{w},b)}{\partial b} \\ &\rbrace \end{align*}$$ where $$\begin{align*} \frac{\partial J(\mathbf{w},b)}{\partial w_j} &= \frac{1}{m} \sum\limits_{i = 0}^{m-1} (f_{\mathbf{w},b}(\mathbf{x}^{(i)}) - y^{(i)})x_{j}^{(i)} + \frac{\lambda}{m} w_j \tag{2} \\ \frac{\partial J(\mathbf{w},b)}{\partial b} &= \frac{1}{m} \sum\limits_{i = 0}^{m-1} (f_{\mathbf{w},b}(\mathbf{x}^{(i)}) - y^{(i)}) \tag{3} \end{align*}$$ # [[无监督学习]] Q: 什么是[[无监督学习]] A: 在一个由输入和没有打上“正确标签”的输出所组成的数据集当中，通过机器学习，用于异常检测，相似数据点组合在一起 # 神经网络 什么是神经网络： 说白了就是人类仿造大脑中神经元的构造，利用逻辑回归，多层嵌套，达到不需要关心里面特征向量是什么，只需要给定输入，就能拿到输出  标记的规定：  输入层为layer 0 隐层层第一层次为layer 1直到输出层。是多少层给【多少】。 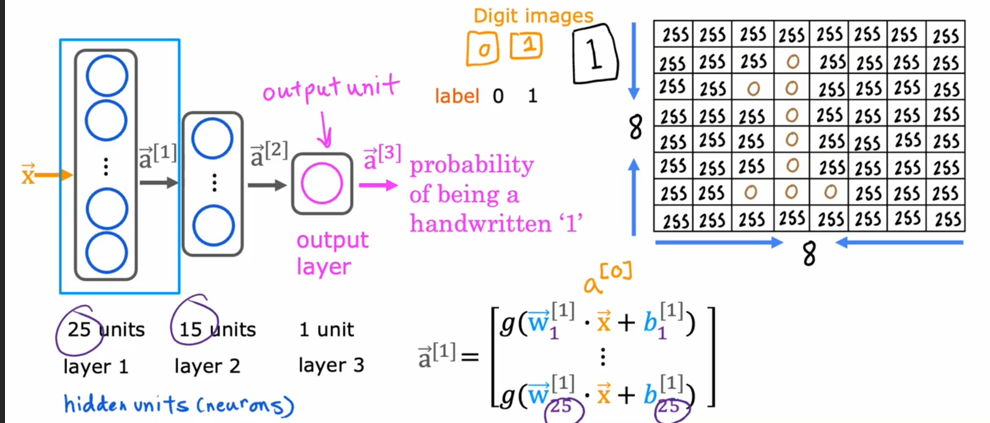 每第i层收到a【i-1】的输入，输出a【i】给下一层 代码的实现：  其中np.array( ? )为什么用的是两个方括号？ Numpy用的是TensorFlow这个库，？是一个二维矩阵 这个库帮我们自动传递a，即每一层activtion function的输出，只需要几行代码就能表达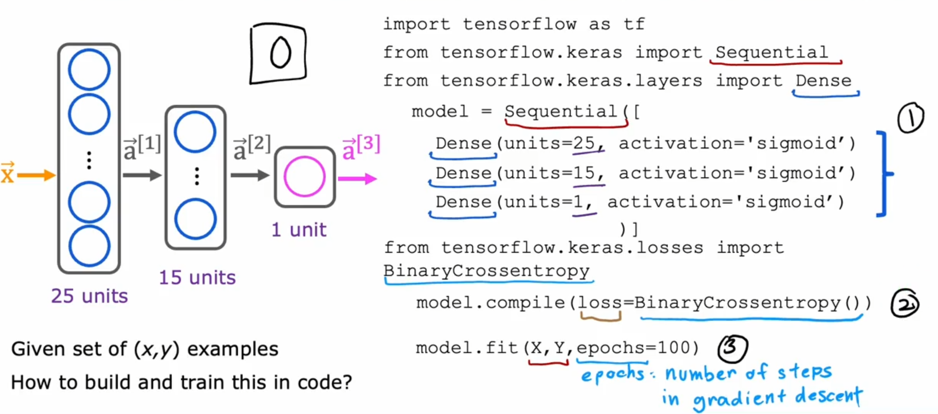：  1. 构造神经网络（units：这一层多少神经元，activation：选择哪一个激活函数，在隐藏层的时候选择 [sigmoid]，[Relu]，在输出层的时候，选择sigmoid,[Softmax],线性等等） 2. 选择Cost Function(或者说Loss Function的平均值) 3. 梯度下降（特征向量，实际值，梯度下降多少次） Q:为什么隐藏层不能选择线性函数？ A: 因为多层线性下来，最后还是一个线性函数，达不到复杂化的效果 其中，[Relu Function]是隐藏层中较为常用的activation function 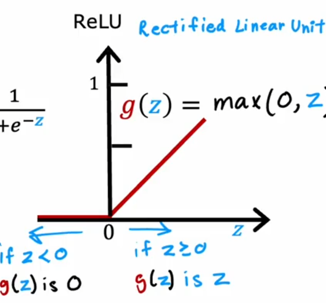 在输出层，我们应该根据实际值y标签去选择输出函数，y只有非负值时，用Relu,y只有两个预测值时，用Sigmoid Function 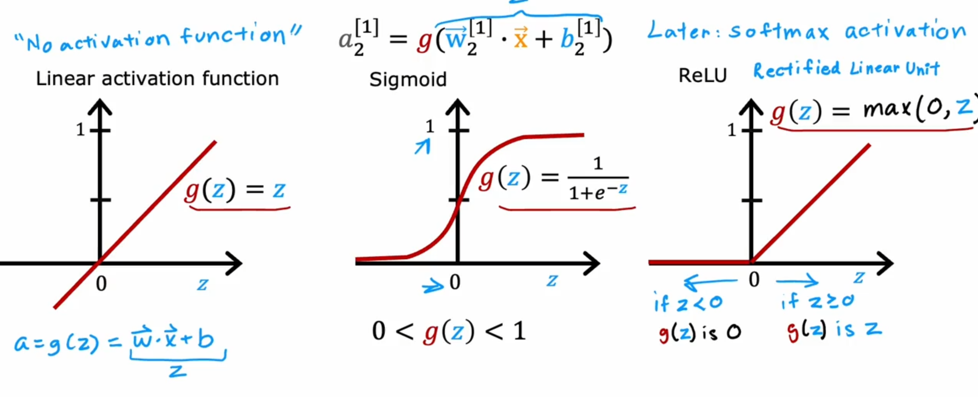 然而当y的值有多个的时候用什么函数呢？用Softmax function。  Softmax function 可以看作Sigmoid Function的推广，把二元推广为多元 输出层的输出为：$$a_j = \frac{e^{z_j}}{ \sum_{k=1}^{N}{e^{z_k} }} \tag{1}$$ 其Loss Function名为：SparseCrossEntropy  为了让Tensorflow在计算的过程中不四舍五入，提高运算的精确度，需要这样写code: 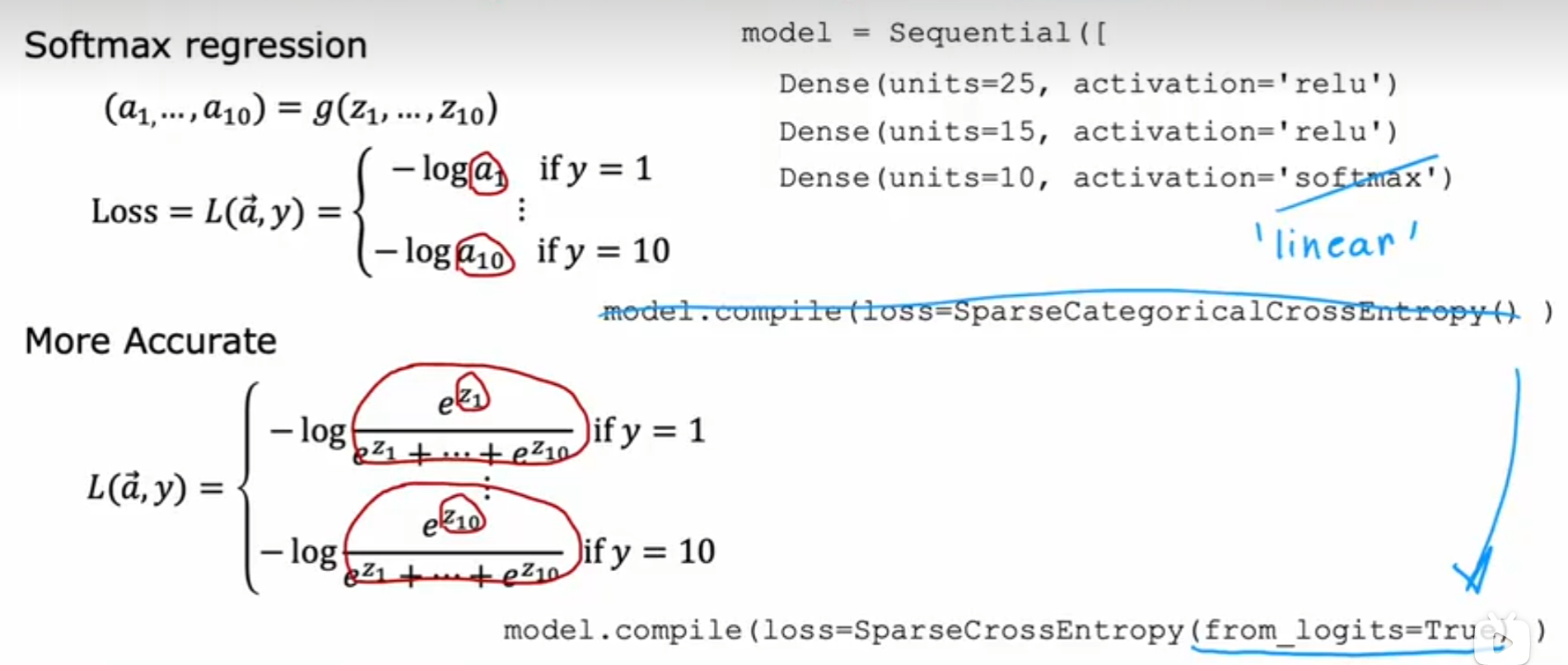 更好的梯度下降的算法  当学习率过高，就减少一点，过低，就增加一点 被称为**Adam算法**，对于每一个学习率都可以分别被执行这个算法  代码实现：  # 模型的选择 ## 选择什么样的模型？ 当我们的模型建立不理想时，往往不知道从如何入手去改善这个模型，以下有几种方法，可以用来改善模型： 4. 更多的训练集 5. 减少模型的复杂程度 6. 加入其他的特征变量 7. 加入特征变量的多项式 8. 减少lambda 9. 增加lambda  对于线性回归的模型评估  比较j train 和 j test 当我们选择模型的时候，例如线性回归到底用几项式？一般我们用训练集得到参数，测试集来判断误差程度，再选取误差最小的模型。  但这样有一个问题是这样选择的模型只是对测试集的最好的模型，不一定能泛化，所以我们需要再分出一个数据集专门用来选择模型（交叉验证集）  先用训练集的数据训练出模型（一个超参数组合对应一个模型），再用交叉验证集的数据选择误差最小的模型，最后用测试集数据验证性能  评估模型时，用是否高偏差（训练集J_train 很大）和高方差（交叉验证集J_cv很大）来评估 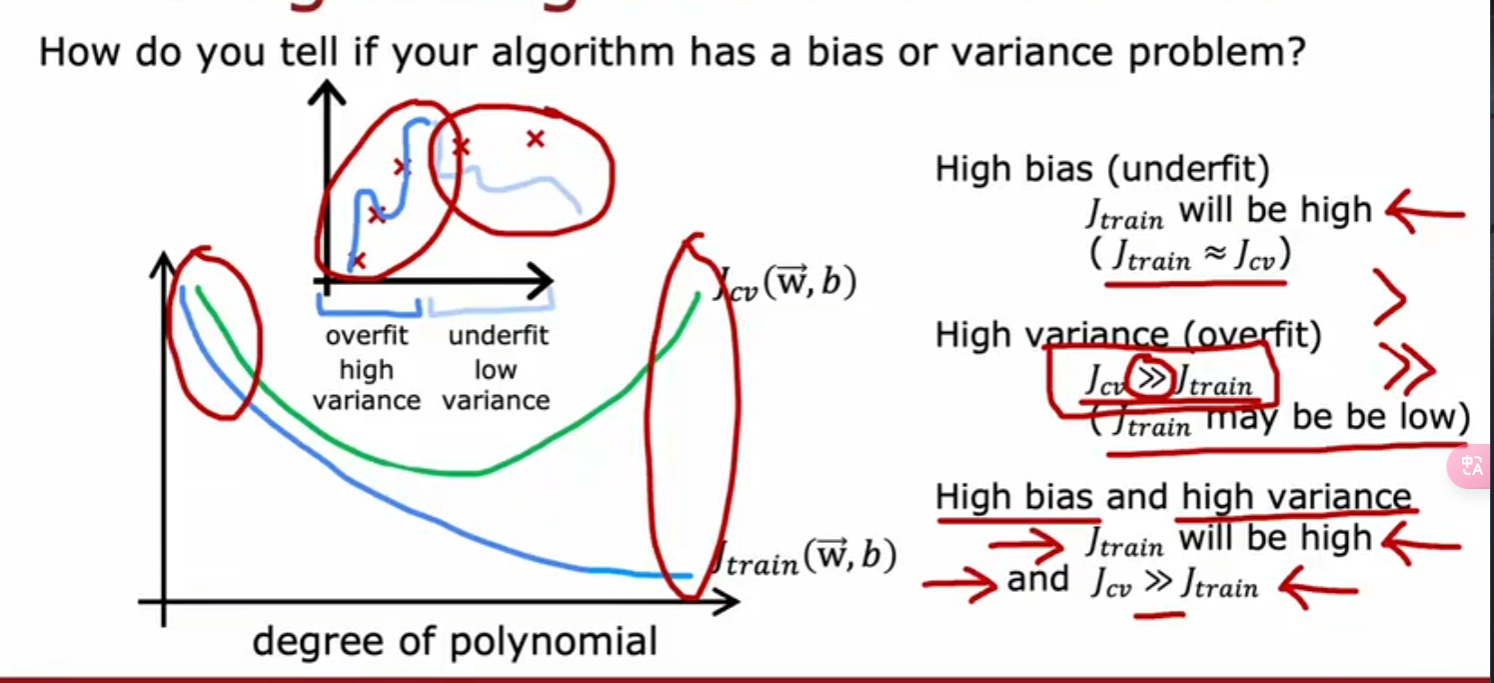 ## 正则化的lambda该如何选择？ 当模型用到了正则化时，对于lambda的选择也很重要，因为它影响了最后的偏差和方差  但高偏差于高方差是有多高呢？ 是相对而言的：  baseline performance可以是人类的误差，又或者是先前算法的误差，高偏差就是相对于base performace而言的，高方差是相对于J_train而言的 ## 什么时候该增加训练数据？ 当模型过于简单时，J_train and J_cv都高于baseline，此时无论如何增加多少数据集，都不能减少偏差  只有模型比较复杂的时候，且是高方差时，增加训练集才有效果 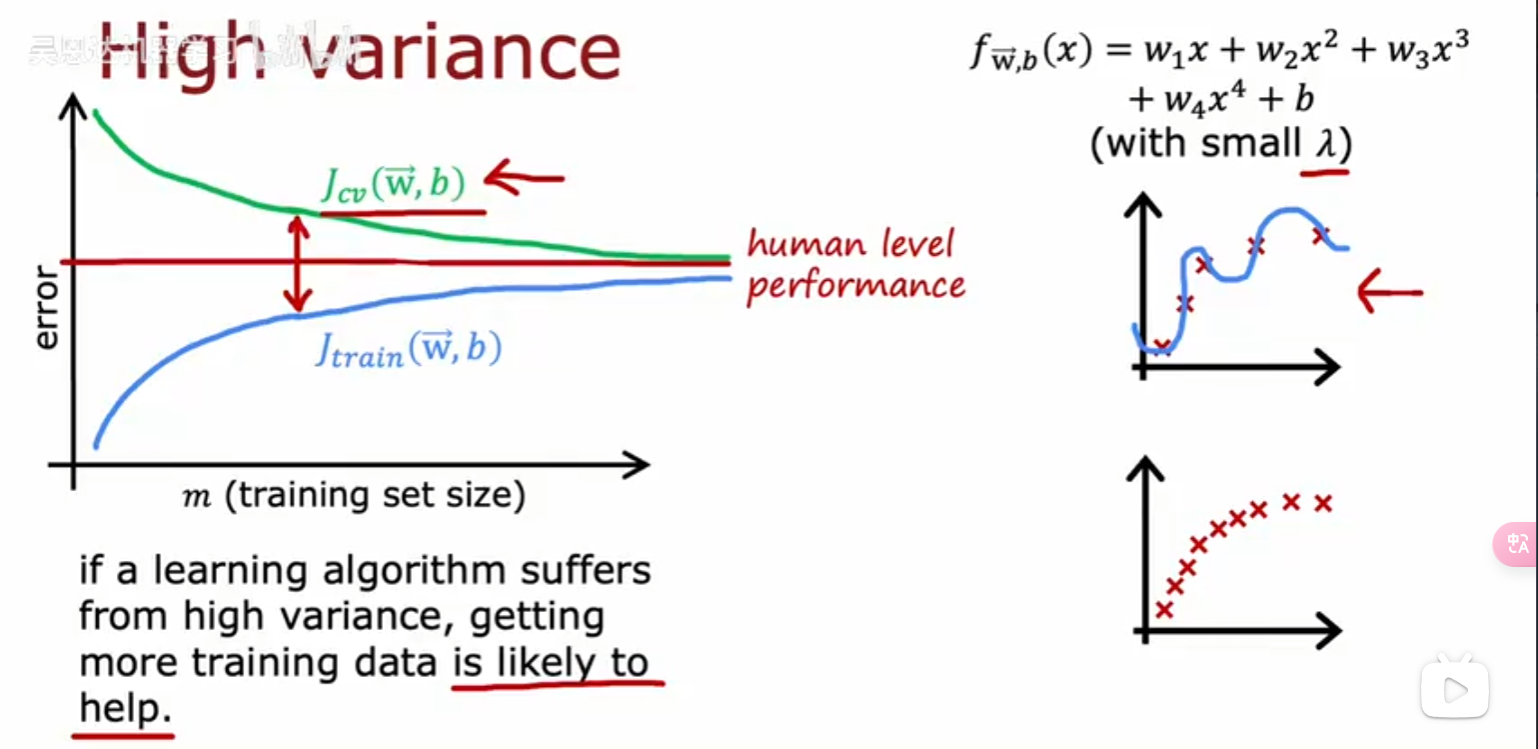 ## 高偏差或高反差分别的解决方案  ### 高偏差：意味着模型过于简单，训练集误差过大 10. 更多的特征变量 11. 更多的特征变量的多项式 12. 减少lambda的值 ### 高方差：意味着模型过拟合，cv集误差过大 1. 更多的训练数据 2. 更少的变量次方 3. 增加lambda的值 ## 神经网络中模型的选择 在神经网络中，往往不需要考虑高偏差与高方差的权衡问题，因为只要神经网络的隐藏层够多，神经元够多，就能以更复杂，更灵活的方式拟合实际的数据，如果高方差了，只需投喂更多数据 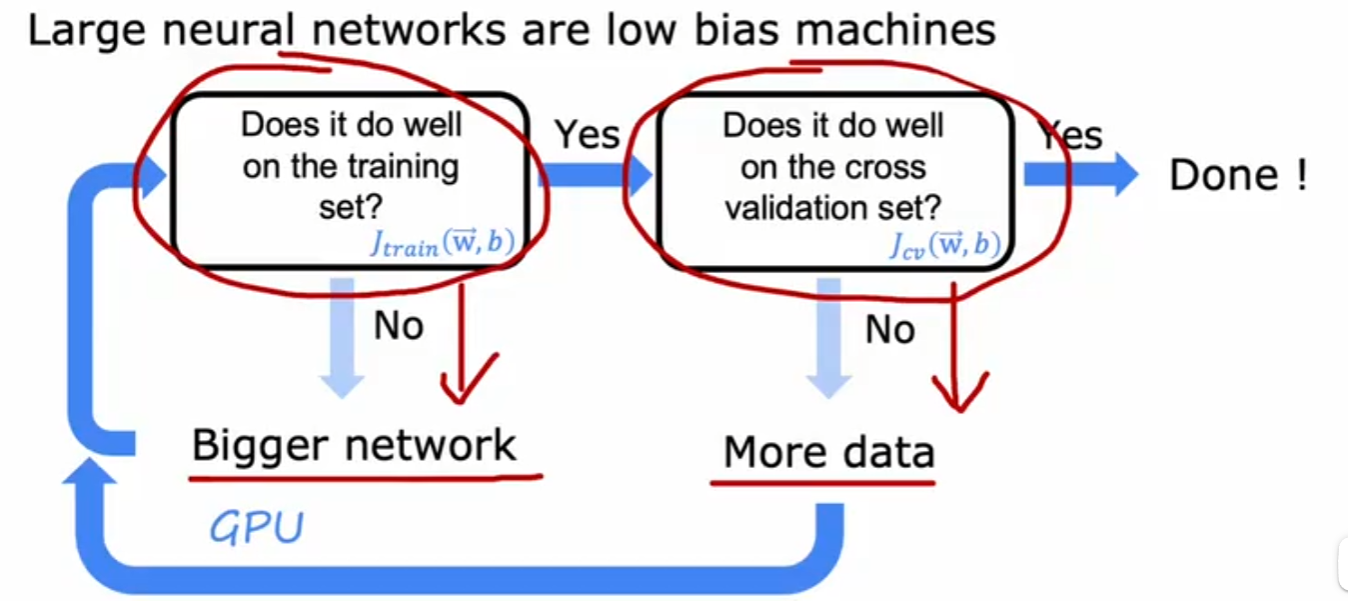 且将每一个隐藏层正则化：  唯一的缺点只是增加了计算量 ## 机器学习模型的构建过程 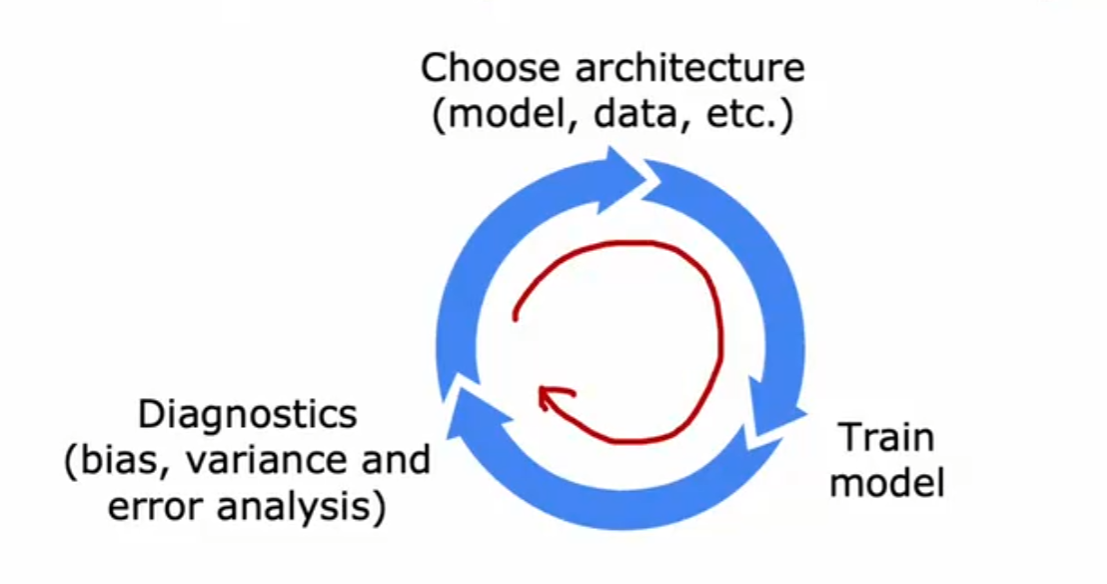 while(true){ 4. 选择模型，数据集 5. 训练模型 6. 查看是高偏差还是高方差 } 例子：识别垃圾邮箱 第一次选择的模型，看邮箱里面是否包含一些显著的关键字来判断是否是垃圾邮箱，但一轮过后模型并不好，有高偏差或者高方差，这时候你可以反思是否模型的选择有问题，比如这个垃圾邮箱还有其他的特征变量，比如邮箱的url，邮箱的路由等等 在选择数据集的时候也有讲究，在现实生活中，可能没有这么多数据供你训练，且创造数据集是费时费力的，此时我们可以通过数据增强的方式，在已有的数据集的基础上扭曲，变形，得到新的，类似的数据集，以供我们训练模型，这种就叫做数据增强  完整的生命周期 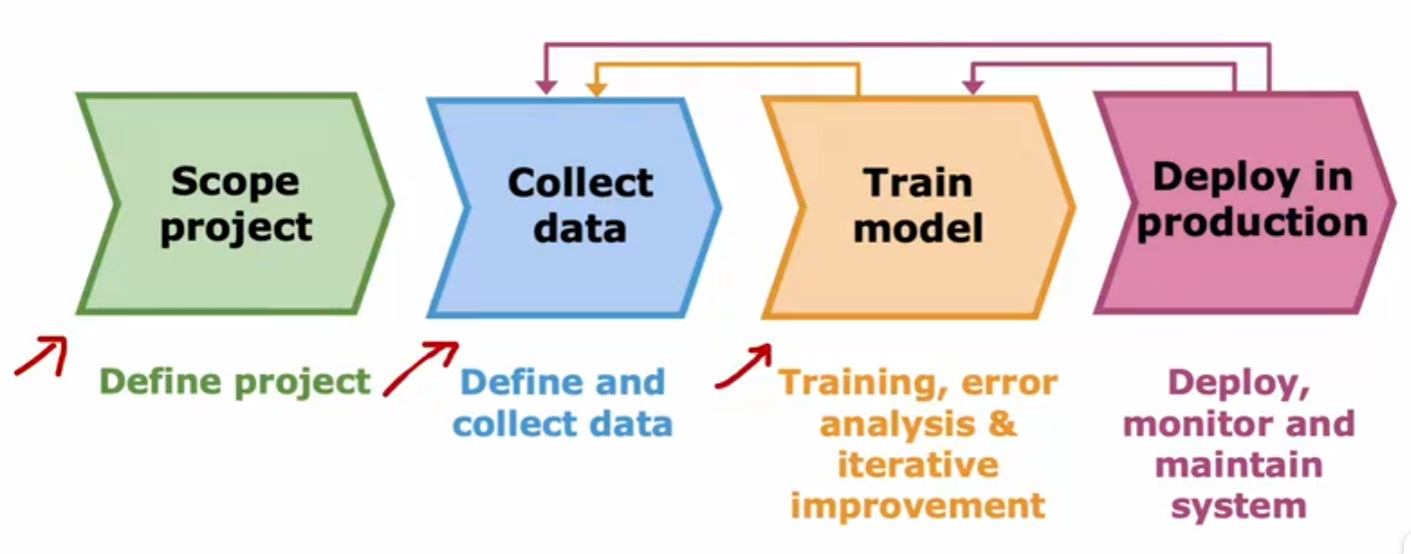 ## 迁移学习 以识别数字为例，我们可以用别人已经用一百万张图片训练的模型的参数，作为我们模型隐藏层的参数，即迁移，然后我们再自己选择输出层的函数，投喂数据训练它们，就能更快，更准确的得到想要的结果 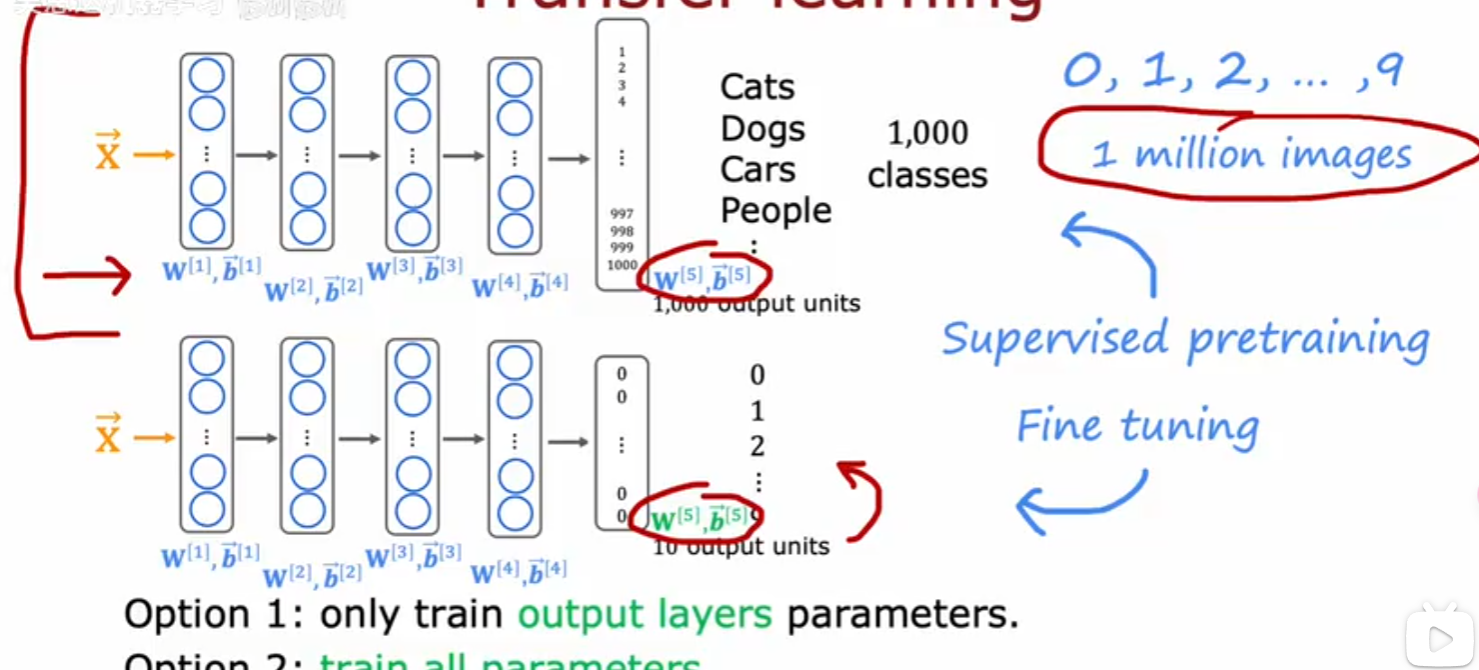  # 模型的评估 精确率和召回率  精确率和召回率的权衡，阈值越高，精确率更高，召回率越低，阈值越低，相反  ## F1_score 取精确率和召回率调和平均数，强调更小的那个数对结果的影响 