最长公共子序列问题(LCS)
给出两个长度分别为n和m的序列A=a1a2.an和B=b1,b2bm,求A和B的最长公共子序列C=C1、C2…Cp 满足: (1)存在一个n1<n2<…<np且ni⇐n, An1 An2…Anp=C (2存在一个m1<m2,<…<mp,且mi⇐m, Bm1Bm2…Bmp=C
例:A=abcbdacb B=bdcab C=bcab
动态规划

注意初始化dp数组的时候行和列需要多增加一个,避免造成索引越界
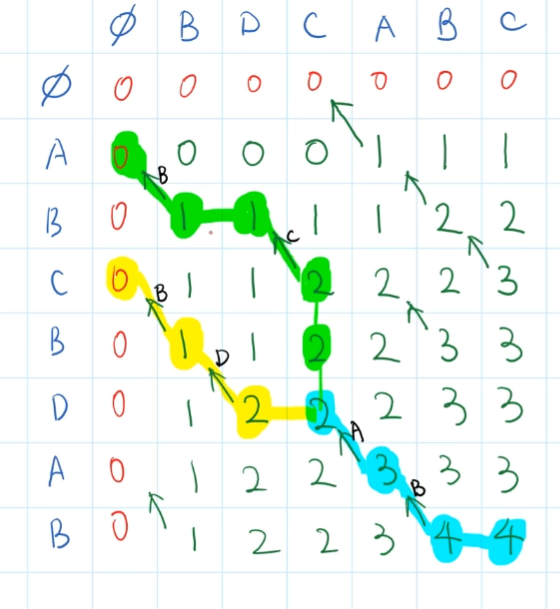
const arr1 = ['a', 'c', 'd', 'c', 'b'];
const arr2 = ['a', 'd', 'c', 'b'];
/**
* 构造 LCS 问题的 DP 二维数组
* dp[i][j] 表示 arr1 的前 i 个字符和 arr2 的前 j 个字符的最长公共子序列的长度。
*/
function initDp(arr1, arr2) {
let dp = [];
const n = arr1.length;
const m = arr2.length;
// DP 数组需要 (n+1) x (m+1) 大小
for (let i = 0; i <= n; i++) {
dp[i] = [];
for (let j = 0; j <= m; j++) {
dp[i][j] = 0; // 初始化所有元素为 0
}
}
// 填充 dp 表
for (let i = 1; i <= n; i++) { // 从 1 开始遍历
for (let j = 1; j <= m; j++) { // 从 1 开始遍历
// 注意:arr1 和 arr2 的索引需要减 1,因为 dp 表的索引是从 1 开始的
if (arr1[i - 1] === arr2[j - 1]) {
dp[i][j] = dp[i - 1][j - 1] + 1; // 字符匹配,长度加 1
} else {
// 字符不匹配,取左边和上边较大的值
dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
}
}
}
return dp;
}
/**
* 根据 DP 表回溯找到最长公共子序列
*/
function lcs(arr1, arr2) {
const dp = initDp(arr1, arr2); // 首先获取正确构造的 dp 表
const n = arr1.length;
const m = arr2.length;
let lcsSequence = []; // 存放最长公共子序列的字符
let i = n; // 从 dp 表的右下角 (dp[n][m]) 开始回溯
let j = m;
// 回溯循环,直到到达 dp 表的边界 (i=0 或 j=0)
while (i > 0 && j > 0) {
// 情况 1: 如果当前字符匹配,则它是 LCS 的一部分
// 同样注意:arr1 和 arr2 的索引需要减 1
if (arr1[i - 1] === arr2[j - 1]) {
lcsSequence.unshift(arr1[i - 1]); // 将字符添加到数组开头(因为是倒着回溯)
i--; // 同时向左上角移动
j--;
}
// 情况 2: 如果字符不匹配,根据 dp 值决定向上还是向左移动
else if (dp[i - 1][j] > dp[i][j - 1]) {
i--; // 向上移动 (arr1 的字符不匹配,所以往前跳过 arr1 的当前字符)
} else {
j--; // 向左移动 (arr2 的字符不匹配,所以往前跳过 arr2 的当前字符)
}
}
return lcsSequence.join(''); // 将字符数组连接成字符串并返回
}
const result = lcs(arr1, arr2);
console.log("最长公共子序列:", result); // 应该输出 "acb"
console.log("dp 表 (用于调试):", initDp(arr1, arr2)); // 可以打印 dp 表来辅助理解